Después de tres décadas de investigación, con la ayuda de una supercomputadora, los matemáticos finalmente descubrieron un nuevo ejemplo de un número entero especial llamado número de dedekind.
Se calcula que solo el noveno de su tipo, o D(9), equivale a 286 386 577 668 298 411 128 469 151 667 598 498 812 366, si actualiza sus propios registros. Este monstruo de 42 dígitos sigue al D(8) de 23 dígitos que fue descubierto en 1991.
El concepto del número de Dedekind es difícil de entender para los no matemáticos, y mucho menos de resolverlo. De hecho, los cálculos involucrados son tan complejos e involucran números tan enormes que no era seguro que alguna vez se descubriera D(9).
«Durante 32 años, calcular D(9) había sido un desafío abierto y era cuestionable si este número podía calcularse». Él dijo El informático Lennart van Hertum, de la Universidad de Paderborn en Alemania, anunció esta cifra el pasado mes de junio.
Está situado en el medio del número de Dedekind. Funciones lógicaso un tipo de lógica que selecciona una salida a partir de entradas que constan de solo dos estados, como verdadero y falso, o 0 y 1.
Las funciones booleanas monótonas son aquellas que restringen la lógica de tal manera que cambiar 0 por 1 en la entrada solo cambia la salida de 0 a 1, no de 1 a 0.
Investigadores característica Usando rojo y blanco en lugar de 1 y 0, pero la idea es la misma.
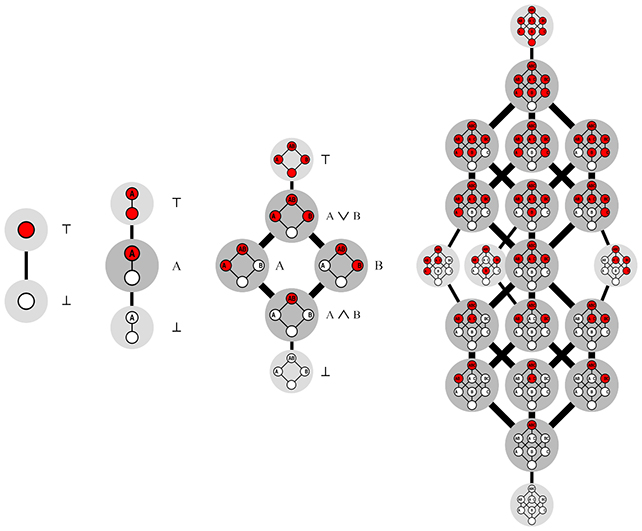
«Básicamente, puedes pensar en una función booleana monótona en dimensiones 2, 3 e infinitas como un juego con un cubo de n dimensiones». Él dijo Van Hertom.
«Puedes equilibrar el cubo en una esquina y luego colorear cada una de las esquinas restantes de blanco o rojo».
«Sólo hay una regla: nunca debes colocar una esquina blanca encima de una esquina roja. Esto crea una especie de intersección vertical entre el rojo y el blanco. El objetivo del juego es contar cuántas piezas diferentes hay».
Los primeros son bastante sencillos. Los matemáticos calculan D(1) como sólo 2, luego 3, 6, 20, 168…
En 1991, fue necesario Supercomputadora Cray-2 (uno de los superordenadores más potentes de la época) y el matemático Doug Wiedemann 200 horas para descubrir D(8).
D(9) terminó siendo aproximadamente el doble de largo que D(8) y requirió un tipo especial de supercomputadora: una máquina que usaba módulos especializados llamados matrices de puertas programables en campo (FPGA) que podían realizar múltiples cálculos en paralelo. Esto llevó al equipo al superordenador Noctua 2 de la Universidad de Paderborn.
«Resolver problemas combinatorios difíciles con FPGA es un área de aplicación prometedora, y el Noctua 2 es uno de los pocos superordenadores del mundo en el que se puede realizar el experimento». Él dice El informático Christian Plessel, director del Centro de Computación Paralela de Paderborn (PC2), donde se guarda Noctua 2.
Se necesitaban más mejoras para darle al Noctua 2 algo con qué trabajar. Utilizando simetrías en la fórmula para hacer el proceso más eficiente, los investigadores le dieron a la supercomputadora una suma enorme para resolverlo, una suma que incluía 5,5*10^18 términos (el número de granos de arena en la Tierra se estima en 7,5*10 ^18 para comparación).
Cinco meses después, Noctua 2 encontró la respuesta y ahora tenemos D(9). Los investigadores no han identificado D(10) por el momento, pero podemos imaginar que podrían pasar otros 32 años hasta encontrarlo.
El trabajo fue presentado en septiembre en Taller internacional sobre funciones lógicas y sus aplicaciones. (BFA) en Noruega.
Una versión anterior de este artículo se publicó por primera vez en junio de 2023.






More Stories
El jefe de la Agencia Espacial de EE.UU. quiere hablar con China sobre la basura espacial
Búsqueda de gemas: caracterización de seis planetas gigantes que orbitan enanas frías
La Administración Federal de Aviación de EE. UU. ha puesto en tierra los cohetes Falcon 9 de SpaceX en espera de una investigación sobre un raro accidente de aterrizaje frente a la costa.